0
￥0
カート
ゾムツール ハイパードゥキット
￥44,000
税込
商品コード： zom0036
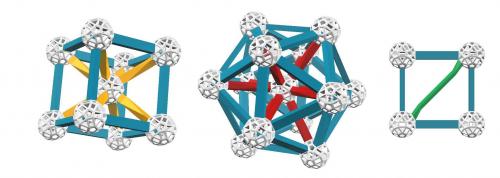
正百二十胞体(Hyperdodecahedron、または、Regular hecatonicosachoron)が作れる大型キットです。完成すると直径が30cm近い球体が出来上がります。
【内容】全970ピース
ノード：330
ストラット：
B0 180
Y0 200、Y1 20
R00 120、R0 120
【対象年齢】6歳以上
【素材】ABS樹脂
ゾムツールについてはこちらもご覧ください。
【内容】全970ピース
ノード：330
ストラット：
B0 180
Y0 200、Y1 20
R00 120、R0 120
【対象年齢】6歳以上
【素材】ABS樹脂
ゾムツールについてはこちらもご覧ください。
ストラットの長さについて
ゾムツールのストラットは「B0」を基本として
自然界に潜む黄金比に基づいて「B1」「B2」が作られています。
(B0:B1=B1:B2=1:1.6180・・・)
そして
「B0」で作られた「立方体(正六面体)」の中心と、立方体の点の長さが「Y0」
「B0」で作られた「正二十面体」の中心と、正二十面体の点の長さが「R0」
「B0」で作られた「正方形」の対角線の長さが「G0」
になるように作られています。
